0 of 15 questions completed
Questions:
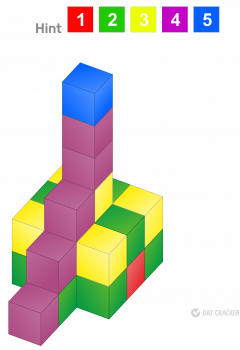
| PART 5 (For questions 1 through 15)Several stacks of cubes have been cemented together to form an entire figure. After being cemented, each cube was varnished on all external surfaces (excluding the bottom). The only hidden cubes are those required to support other cubes.You must determine the number of cubes in the figure that have a particular number of varnished sides. *only one of their sides painted *only two of their sides painted *only three of their sides painted *only four of their sides painted *all five of their sides painted Note: There are no problems for which zero (0) is the correct answer.There are five possible answer choices for this PAT section.Here are the rules:
Try the following example: In this figure, how many cubes have two of their exposed sides painted?
Click Begin Exam to get started. |
You have already completed the quiz before. Hence you can not start it again.
Exam is loading ...
You must sign in or sign up to start the exam.
You have to finish following exam, to start this exam:
0 of 15 questions answered correctly
Your time:
Time has elapsed
You have reached 0 of 0 points, (0)
| Average score |
|
| Your score |
|
Estimated DAT PAT Score: Less than 15
Just know, when you truly want success, you’ll never give up on it. No matter how bad the situation may get. Keep your head up and keep on fighting!
Estimated DAT PAT Score: 16
You’re on the right track. Take your time to reflect on your performance and how you can improve your scores the next time around. Carefully review these solutions, learn from your mistakes and understand the intricacies of each question. Try to visualize the question and solution in your mind. You’re going in the correct direction and you’ll only go up from here!
Estimated DAT PAT Score: 17
You’re doing a good job! Keep working on it and you’ll soon see your score in the 20’s. Take your time in understanding your mistakes and in carefully reviewing these solutions and learning from he intricacies of each question.
Estimated DAT PAT Score: 18
Good going! You are really getting to where you need to be. Keep it going! Keep on working on it and you’ll soon see your score in the 20’s. Take your time in understanding your mistakes and in carefully reviewing these solutions and understanding the intricacies of each question. Your goal should be to beat your 18 on the next test!
Estimated DAT PAT Score: 19
Awesome job! Keep it up and you’ll soon be in the 20’s. Learn from your mistakes and strategize on how you’ll beat your 19!
Estimated DAT PAT Score: 20
Awesome job! You did it! You hit the 20 mark. You really outdid yourself today.
Estimated DAT PAT Score: 21
Impressive! You’re coming along very nicely!
Estimated DAT PAT Score: 22
You rocked it! That was quite an accomplishment!
Estimated DAT PAT Score: 23
You are a rockstar! We tip our hats to you!
Estimated DAT PAT Score: 24 or higher
You’re golden!
| Pos. | Name | Entered on | Points | Result |
|---|---|---|---|---|
| Table is loading | ||||
| No data available | ||||
61.
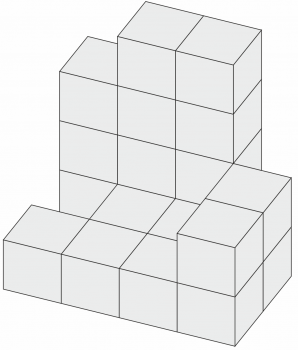


62.



63.



64.
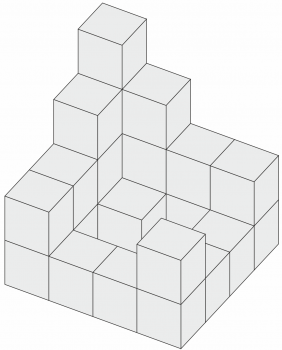
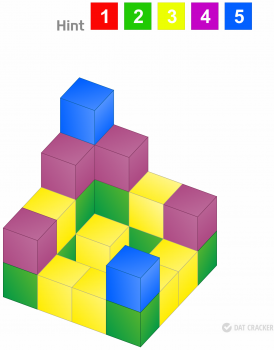

65.



66.



67.
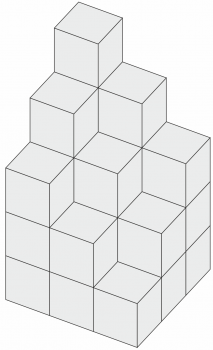
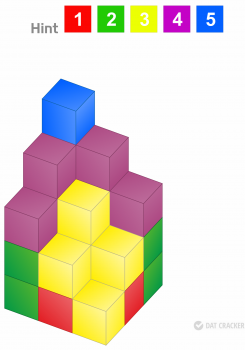

68.



69.



70.
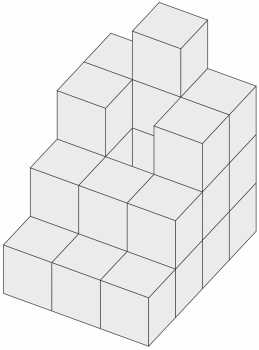
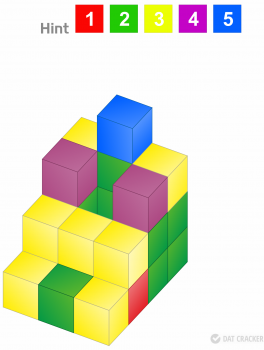

71.



72.



73.
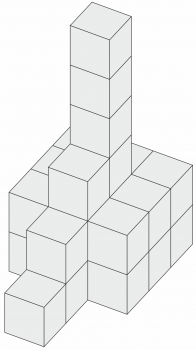

74.



75.




